Y llegó Einstein, y la masa se hizo energía.

Piensa en la primera ecuación que te venga a la cabeza. Seguro que estás pensando en la misma que yo. Vale, la cosa es un poco absurda pues si estás leyendo esto ya te habrás fijado ella. La has visto infinidad de veces. Es la más famosa de todos los tiempos. Como ya sabes, nos referimos a la archiconocida ecuación:

Ecuación 1

¿Entiendes realmente su significado? ¿Sabes cómo se llega a ella?

Esta entrada es continuación de dos entradas anteriores del blog sobre la Teoría de la Relatividad Especial del genial Albert Einstein. Hablamos de “Teoría de la Relatividad de Einstein… ¡Qué Especial eres!" y “¿Qué es el Espacio-Tiempo?” Si no las has leído te recomiendo que lo hagas. Con esta entrada finaliza esta serie, en la que hemos intentado dar una idea general sobre la fascinante Teoría de Relatividad Especial de Einstein. En la primera entrada deducimos a partir de relaciones matemáticas muy sencillas la ecuación de la dilatación temporal, poniendo de manifiesto que el tiempo es diferente dependiendo de la velocidad.

Ecuación 2. Esta ecuación pone de manifiesto que un observador verá pasar el tiempo más despacio de otro, que se mueve a una cierta velocidad. A velocidades pequeñas respecto a las de la luz,  el factor de Lorentz = 1, por lo que t = T

Tras descubrir que tiempo y espacio no son absolutos, es decir, que diferentes observadores no tendrán por qué medir los mismos valores de estas magnitudes, en la segunda entrada iniciamos una búsqueda de magnitudes invariantes (que no cambian su valor, independientemente de quién sea el observador). En ella descubrimos como la combinación del espacio con el tiempo nos conduce a una representación de la realidad con cuatro dimensiones (tres espaciales y la temporal) en la que podemos medir una magnitud, las distancias espacio-temporales, en las que todos los observadores están de acuerdo, es decir, que obtienen el mismo valor. Vimos que tiempo y espacio son relativos, maleables, pues dependen de la velocidad del observador, pero sin embargo, en la combinación de ambos las distancias espacio-temporales entre dos eventos medidas por diferentes observadores dan como resultado el mismo valor.

Figura 1. En el espacio-tiempo tetradimensional, diferentes observadores que se mueves a una cierta velocidad entre ellos, medirán diferentes valores de espacio (x_A y x_A’) y tiempo (t_A y t_A’) para un mismo evento (A, A’), pero sin embargo, el valor de “s” que calculen ambos (la longitud de la flecha), será el mismo.

Ecuación 3

Con estas dos entradas hemos puesto los cimientos para poder avanzar hacia la obtención de la famosa ecuación. La pregunta que nos hacemos ahora es si en el espacio-tiempo habrá otras cantidades invariantes, es decir, que no dependan de la velocidad de los observadores. Descubriremos que sí, y ello nos conducirá a la deducción de la ecuación. Si logramos entender el proceso, cosa que espero, tendrás la gran satisfacción de haber conseguido comprender una gran parte de esta fascinante teoría, tan conocida como incomprendida. Vamos allá.

En nuestra búsqueda de nuevas cantidades invariantes en el espacio-tiempo examinaremos una nueva medida de una magnitud que se conoce desde hace muchísimos años: la cantidad de movimiento o momento lineal. El momento lineal es una magnitud física que depende de la velocidad de un objeto y su masa. Todos sabemos que no tiene el mismo efecto el impacto de una pequeña bola de papel que se mueve a 40 km/h, que un camión de 20 toneladas que se mueva a esa misma velocidad. La experiencia pone de manifiesto que los efectos de las colisiones de unas cosas con otras dependen tanto de sus masas como de sus velocidades. Pues bien, en física clásica se define el momento lineal como el producto de la masa por la velocidad:

Ecuación 4

De esta manera, por ejemplo, un objeto de 1 kg que se mueva a 5 m/s tendrá un momento lineal de 1x5 = 5 kgm/s.

Esta ecuación resulta muy útil porque una propiedad importante de la magnitud momento lineal es que se conserva: es lo que denominamos ley de conservación del momento lineal. Esto quiere decir que, por ejemplo, en la colisión de dos objetos que se mueven a distinta velocidad (y tienen, por tanto, diferentes momentos lineales) la resultante (suma) de los momentos lineales de los dos objetos debe tener el mismo valor antes y después del choque. 

Un ejemplo del cumplimiento de este principio es el sistema formado por un cañón-bola de cañón: antes del disparo el momento lineal total es cero pues los momentos lineales de la bola y el cañón son cero, ya que sus velocidades son nulas. La Ley de Conservación del Momento Lineal nos dice que después del disparo el momento lineal total también debe ser cero: esta es la razón por la que el cañón experimenta un retroceso:

Figura 2

Las leyes de conservación son muy útiles en física, en general cuantas más leyes de conservación podamos aplicar a un problema, más fácil resultará encontrar su solución. Hay otra ley de la conservación muy importante: la Ley de la conservación de la energía. Esta ley, conocida desde hace mucho tiempo también, básicamente quiere decir que la energía no puede crearse ni destruirse, sino que únicamente puede cambiar de una forma de energía a otra.

Una de las formas en las que puede manifestarse la energía es mediante la energía cinética: es la energía asociada a una partícula en movimiento debido a su velocidad. La expresión para calcular la energía cinética viene dada por la siguiente expresión:

Ecuación 5

Así, conociendo la masa y la velocidad de un objeto, podemos calcular su energía cinética asociada. Cuanto mayor sea la velocidad de un objeto, mayor será su energía cinética.

De momento dejaremos aparcada la energía para centrarnos en el momento lineal. Nuestra tarea ahora será la de encontrar el equivalente del momento lineal como magnitud invariante en el espacio-tiempo.

En el espacio tridimensional (sin tener en cuenta la dimensión temporal), el momento se puede representar mediante un vector:

Figura 3

Un vector no es más que la representación de una magnitud que tiene una dirección concreta. En el ejemplo de la Figura 2, un objeto esférico con masa m se ha desplazado una cierta distancia (Δx) en un intervalo de tiempo (Δt), por lo que su velocidad será Δx/Δt. La flecha representa al vector momento lineal, cuyo valor (longitud de la flecha) se obtiene multiplicando la masa del objeto por su desplazamiento y dividiéndola por el intervalo de tiempo, y cuya dirección es la que indica la dirección de la flecha.

Según la ecuación 4, el momento vendría dado por:

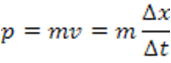Ecuación 6

La cuestión ahora será encontrar un sustituto de esta expresión para nuestro espacio-tiempo tetradimensional, mediante el empleo de magnitudes invariantes. Tal como vimos en la entrada anterior y en la ecuación 3, la distancia invariante en el espacio-tiempo viene dada por:

Ecuación 7. El símbolo Δ (incremento), indica que se trata de intervalos, es decir, una diferencia entre un estado inicial y final.

Recuerda que “Δs” es la única distancia que no cambia para los posibles observadores (cosa que no sucede con “Δt” y “Δx”, pues diferentes observadores podrán medir diferentes valores de ellos). Como en la obtención del vector momento lineal en el espacio-tiempo debemos utilizar cantidades invariantes, la distancia “Δx” que aparece en la ecuación del momento lineal en el espacio tridimensional (ecuación 6) deberemos sustituirla por “Δs” en el espacio-tiempo. Ya hemos avanzado algo pero, ¿cuál será el sustituto del “Δt” para nuestro espacio-tiempo? Debemos coger una cantidad invariante y que además tenga unidades de tiempo, por ejemplo segundos. En nuestro modelo de cuatro dimensiones hay una única posibilidad: la magnitud correspondiente a “Δt” del espacio tridimensional para nuestro espacio-tiempo es el cociente entre “Δs” y “Δc”. Ambas son cantidades invariantes y su cociente da como resultado unidades de tiempo: 

Repetimos, pues es una de las claves para poder continuar: para la construcción del vector momento en nuestro espacio-tiempo debemos sustituir Δx y Δt de la ecuación 6 por las siguientes magnitudes invariantes:

Figura 4

De esta manera, la expresión del momento queda como:

Ecuación 8

Es decir:

Ecuación 9

El valor del vector momento lineal en el espacio-tiempo es el producto de la masa del objeto por la velocidad de la luz, una ecuación semejante a la del momento en el espacio de tres dimensiones (p = mv), pero en la que la velocidad que utilizamos ahora es la velocidad de la luz. Si has leído el anterior post, esto no debería sorprenderte: la velocidad a la que se mueven los objetos a través del espacio-tiempo es la velocidad de la luz, “c”.

De esta manera nuestra flecha del momento en el espacio-tiempo tendrá un valor de "mc" y apuntará en la dirección en la que el objeto viaja a través del espacio-tiempo.

Figura 5

Casi hemos construido nuestro vector momento en el espacio-tiempo, pues todavía nos falta encontrar sus expresiones en los ejes espacial y temporal. Para ello, antes debemos fijarnos con más detalle en la expresión de Δs/c, nuestro sustituto de “Δt” que aparece en la ecuación 6.

Teniendo en cuenta la ecuación 7:

Ecuación 10

Ecuación 11

Y teniendo en cuenta la expresión de gamma (ecuación 2):

Ecuación 12. Gamma cuantifica cuanto se ralentiza el tiempo para alguien que observa a un reloj en movimiento. Tal como explicamos en el primer post, si la velocidad “v” es pequeña, la expresión será igual a la unidad, lo que significa que no habrá apenas retraso en el reloj,  tal como ocurre en la mayoría de las experiencias cotidianas.  

El equivalente a Δt de la ecuación 6 en nuestro espacio-tiempo podemos expresarlo como sigue:

Ecuación 13

Es decir, el equivalente al intervalo de tiempo en nuestro espacio-tiempo es igual a:

Ecuación 14

Con estas herramientas ya estamos en disposición de poder definir completamente el vector momento en nuestro espacio-tiempo, obteniendo las expresiones de las componentes en el eje espacial y temporal.

Para la obtención de las componentes del vector momento en las direcciones espacial y temporal procederemos de la misma manera que con el vector momento lineal en el espacio tridimensional. Recuerda: el valor del vector momento lineal (la longitud de la flecha), se obtiene multiplicando la masa del objeto por su desplazamiento y dividiéndola por el intervalo de tiempo. De esta manera, si partimos de la representación del desplazamiento “s” en nuestro diagrama espacio-temporal, tal como vimos en la entrada anterior:

Figura 6

El vector momento lineal tendrá la misma dirección que “s”, un tamaño de “mc” y para el cálculo de las componentes en el eje espacial y temporal bastará con multiplicar las distancias en los ejes (“x” y “ct”) por la masa y dividir por el equivalente a Dt en nuestro espacio-tiempo, que como hemos visto es igual a Δs/c = Δt/gamma. De esta manera las componentes del vector momento quedan como sigue:

-                                      -  Componente del vector momento en el eje espacial:

    

    

     

Ecuación 15

-                                     -  Componente del vector momento en el eje temporal:

    

      

     

Ecuación 16

      

   De esta manera la representación del vector momento en nuestro espacio-tiempo sería:

      

Figura 7

       

      La componente en eje espacial es igual a gammaxmv. Si te fijas, ésta es una expresión mejorada de la correspondiente en el espacio tridimensional (mv) que incluye al factor de Lorentz (gamma) como corrección. Así, para velocidades pequeñas gamma tiene un valor de 1 y la expresión queda como “mv”. El resultado es muy interesante, pues para velocidades pequeñas obtenemos la expresión correspondiente al momento lineal en física clásica, pero aún más interesante es lo obtenido en el eje temporal.

Estamos ya muy cerca de la obtención de E = mc². Para esto, nos centraremos ahora en la componente del vector en el eje temporal: “gammaxmc”.

Recuerda que el momento lineal es interesante para nosotros porque se conserva. Esto quiere decir que si un conjunto de partículas se mueven a cierta velocidad y colisionan, los momentos de cada partícula serán en general diferentes a los de antes de la colisión, pero la suma total de todos ellos será la misma que la de antes de la colisión. Si el momento se conserva, se deben conservar también las componentes del momento en los dos ejes (espacial y temporal). Así, aplicando la ley de la conservación para el momento en la dirección espacial obtenemos la antigua ley de conservación del momento en física clásica, pero mejorada con el Factor de Lorentz (gamma) , que depende de la velocidad.

Y para el eje temporal hemos obtenido otra ley de conservación: la conservación de “gammaxmc”.

Sigamos el siguiente razonamiento, ya queda poco:

Si gammaxmc se conserva también debe hacerlo gammaxmc² pues lo único que hacemos es multiplicar por una constante, “c”.

¿Y qué representa gammaxmc²?

Para velocidades pequeñas gamma puede sustituirse por la siguiente expresión:

Ecuación 17

Esta aproximación es especialmente eficaz para velocidades “pequeñas”. Tanto más precisa cuanto menor sea la velocidad. Por ejemplo, a una velocidad de una décima parte de la velocidad de la luz, el valor de gamma utilizando las dos expresiones da como resultado 1’00504 y 1’00500 respectivamente, unos valores muy parecidos. Estamos hablando de una décima parte de la velocidad de la luz, es decir, una velocidad de 30.000 km/s, unos 100 millones de km/h. Realmente es una velocidad altísima desde nuestro punto de vista. Y a menor velocidad, la precisión es aún mayor.

Si sustituimos la aproximación de la ecuación 17 en la expresión gammaxmc²:

Ecuación 18

Puede que todavía no seas consciente, pero si me has seguido hasta aquí, ya tienes ante tus ojos el significado de la famosa ecuación.

Presta atención:

Para velocidades pequeñas respecto a la luz la expresión indicada en la ecuación 18 se conserva. Como hemos visto en la ecuación 5, 1/2mv²  es la expresión de la energía cinética, que mide la cantidad de energía que tiene un objeto debido a su velocidad. Así pues hemos encontrado una nueva expresión de conservación que consta de una primera parte mc² y una segunda parte que corresponde con una energía, por lo que parece razonable identificar esta expresión con la energía, sólo que ahora la energía consta de dos partes, una debida a la velocidad del objeto y la otra debido a únicamente a su masa. En resumen, gammaxmc², es la expresión de conservación de la energía en el espacio-tiempo.

¿Y cuál es la energía de un objeto que se encuentra en reposo? Si la velocidad, “v”, es nula, como hemos visto gamma tiene un valor de uno, por lo que la expresión de la energía para un objeto en reposo es:

Aquí está. Hemos deducido la ecuación. Lo que la ecuación nos indica exactamente es que la energía de un objeto en reposo es igual al producto de su masa por la velocidad de la luz al cuadrado.

Hemos visto que la representación del momento lineal en el espacio-tiempo nos conduce, no sólo a una nueva versión mejorada de la conservación del momento lineal sino a una también mejorada versión de la conservación de la energía.

Observa la ecuación 18. Imagina un conjunto de partículas en movimiento. Lo que la ecuación nos indica es que al sumar la energía cinética de todas las partículas más su masa multiplicada por “c” al cuadrado, obtenemos algo que no varía. Pero no sólo indica esto, sino que además esconde otra consecuencia mucho más fascinante: no hay nada en contra de la posibilidad de que parte de la masa se transforme en energía cinética y viceversa, siempre que su suma se conserve.

Masa y energía son intercambiables entre sí, y la energía que teóricamente podemos extraer de una masa “m” en reposo viene dada por la ecuación E = mc².

Antes de Einstein, masa y energía parecían totalmente independientes, tras Einstein, descubrimos que masa y energía son manifestaciones de una misma cosa. Tras Einstein descubrimos que es posible transformar masa en energía, y viceversa. De hecho, este fenómeno ocurre constantemente en la naturaleza y sin él, no estaríamos aquí.

Piensa en el proceso de combustión de un trozo de carbón. Tras el mismo, si fuésemos capaces de poder pesar todos los productos obtenidos (cenizas y gases de combustión) comprobaríamos que la masa ha disminuido un poco. Una cantidad tan minúscula que nadie había reparado en ella antes de Einstein. Sin embargo, esa minúscula cantidad es precisamente la que ha dado lugar al calor desprendido en la reacción de combustión, ya que esa minúscula cantidad de masa se ha transformado en calor. El calor generado cuando quemamos un combustible proviene de la transformación de una pequeñísima parte de la masa en energía. Pongamos un ejemplo con números para entenderlo mejor:

Si quemamos 1 kg de carbón se desprenden aproximadamente 17 millones de Julios de energía en forma de calor (la unidad de energía es el Julio). La energía desprendida proviene de la transformación de una parte de la masa en energía. Así, podemos calcular la cantidad de carbón que ha sido transformada en energía mediante la ecuación E = mc² m=E/c²= 17.000.000/(300.000.000)² = 0,0000000002 kg (menos de una millonésima de gramo). Como puedes apreciar, una minúscula cantidad de masa da lugar a una gran cantidad de energía.

Una manera más eficiente de aprovechar la relación entre masa y energía se da en el interior de la tierra o en las centrales nucleares, mediante la fisión nuclear (proceso en el que átomos pesados se dividen en otros más ligeros, con desprendimiento de energía). Como en una reacción de combustión, la suma de la masa de los productos es inferior a la de los reactivos, y la diferencia es lo que se ha transformado en energía. Otro ejemplo se da en los objetos astronómicos más importantes para la vida en el Cosmos: las estrellas. En el interior de las estrellas se dan reacciones nucleares de fusión (combinación de átomos ligeros para formar átomos más pesados) en las que se obtienen energías del orden de un millón de veces superior a la producida en los procesos de combustión. En nuestro sol, cada segundo se transforman 4 millones de toneladas de masa en energía. Aún así, la transformación de masa en energía en estos procesos sigue representando un porcentaje ridículo de la masa total. Como vemos, la transformación completa de masa en energía es extremadamente difícil. Sin embargo, hay un proceso en el que dicha transformación se produce de forma completa: es el proceso de aniquilación de una partícula con su antipartícula, como la aniquilación positrón-electrón. Esta sería una buena forma de obtener energía, pero desgraciadamente la energía necesaria para la obtención de una antipartícula supera con creces a la producida en la aniquilación.

Como último ejemplo, bastante espectacular, citaremos el Gran Colisionador de Hadrones (LHC) del CERN situado en la frontera franco-suiza, donde se hacen chocar protones  que viajan casi a la velocidad de la luz, provocando un gran desprendimiento de energía que da lugar a la formación de otras partículas. No hay lugar sobre la Tierra donde se ponga más de manifiesto la comprobación experimental de la ecuación de Einstein. En el LHC parte de la energía tras la colisión se transforma en nuevas partículas y parte en energía cinética de esas mismas partículas. 

Un último apunte sobre la ecuación. En la misma aparece “c”, la velocidad de la luz. Parece como si la luz jugara un papel fundamental en la propia estructura del espacio-tiempo y en la energía-masa. De hecho es así, pero no en el sentido que crees. Olvida por un momento la definición habitual de “c” como la velocidad de la luz y asimílala a la siguiente: la constante “c” es un límite cósmico de velocidad que no puede ser superado.

Supón una partícula sin masa que viaja a una velocidad cuyo valor es este límite cósmico, “c”. En principio podrías pensar que no puede llevar ninguna energía asociada, pues si “m” es cero, de la ecuación E = mc², obtendríamos que E sería 0. Pero hay un detalle importante: si la masa es nula el valor de gamma se hace infinito (puedes comprobarlo en la ecuación 12), por lo que el valor de la energía queda como la multiplicación de 0 por infinito (E = gammaxmc² = infinitox0), obteniendo lo que en matemáticas se denomina una indeterminación. Esto quiere decir que el producto no tiene por qué dar como resultado cero, de hecho, para este caso particular (m = 0 y v = c) la energía no es cero. Lo que sucede es que toda la energía asociada a una partícula sin masa es empleada por la misma en forma de energía cinética, adquiriendo el máximo valor que puede darse en el Universo para la velocidad: “c”. Es una manera diferente de entender “c”. El valor de “c” no surge como consecuencia de la existencia de la luz, más bien la velocidad de la luz tiene un valor de “c” porque al estar formada por partículas sin masa, se ven obligadas a viajar con una velocidad correspondiente al valor del límite cósmico.

Hasta aquí con la Teoría de la Relatividad Especial de Einstein. A lo largo de tres entradas hemos ido construyendo la teoría hasta llegar a la ecuación más famosa de la historia. A partir de únicamente dos sencillos principios, el de que “el valor de la velocidad de la luz es una constante independientemente de la velocidad de la fuente emisora de luz” y el de que “las leyes físicas deben ser las mismas para todos los sistemas inerciales (sistemas con velocidad constante)” hemos deducido la expresión de la dilatación temporal, hemos pasado de una concepción de espacio y tiempo como magnitudes independientes a un nuevo escenario combinación de los mismos: el espacio-tiempo, y por último, a partir de este nuevo escenario hemos descubierto como la masa y la energía tampoco son magnitudes independientes, sino que forman parte de un mismo fenómeno.

Una vez más, se pone de manifiesto hasta que punto nuestra escala condiciona lo que percibimos como “realidad”. Pero ésta es mucho más rica y fascinante de lo que apreciamos…

Como nota final, tenemos que decir que toda esta teoría está desarrollada para sistemas inerciales, sin aceleración. Pero está claro que en el Universo entran en juego también las aceleraciones, sin ir más lejos tenemos la aceleración de la gravedad. A Einstein le costó varios años introducir la gravedad en su teoría, lo que le condujo a la Teoría de la Relatividad General...

Bibliografía: ¿Por qué E = mc²? Brian Cox y Jeff Forsaw. ISBN: 978-84-9992-296-6    

“Esta entrada participa en la edición LX (marzo-abril de 2015) del Carnaval de la Física cuyo blog anfitrión es ::ZTFNews.”